Determine Which Families of Grid Curves Have a Constant and Which Have V Constant. U Constant

SIFT(Calibration-invariant feature transform)

In this commodity, I will give a detailed caption of the SIFT algorithm and its mathematical principles.

I hope you lot will empathize these after your reading🤔:

1. The main steps of SIFT
2. Why we need to multiply the LoG by σ² to get the calibration invariance
3. Appromixing LoG using Canis familiaris
4. why nosotros apply Hessian to reject some features located on edges.

SIFT is proposed by David G. Lowe in his newspaper. ( This newspaper is piece of cake to understand, I recommend you lot to have a await at it ).

In general, SIFT algorithm tin be decomposed into four steps:

1. Feature point (also called keypoint) detection
2. Feature betoken localization
3. Orientation consignment
4. Feature descriptor generation.

And this commodity volition also follow these steps.

Characteristic signal detection

As its proper name shows, SIFT has the belongings of calibration invariance , which makes information technology better than Harris. Harris is not scale-invariant, a corner may become an edge if the scale changes, as shown in the following image.

Harris is non scale-invariant

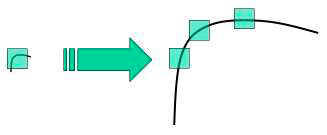
So what i s calibration, and what does scale invariance hateful?
An splendid explanation is given in Tony Lindeberg's paper:

An inherent belongings of objects in the globe is that they simply exist as meaningful entities over certain ranges of calibration. A simple example is the concept of a branch of a tree, which makes sense but at a calibration from, say, a few centimeters to at most a few meters. It is meaningless to talk over the tree concept at the nanometer or the kilometer level. At those scales it is more relevant to talk about the molecules that form the leaves of the tree, or the forest in which the tree grows. Similarly, it is merely meaningful to talk most a deject over a certain range of fibroid scales. At effectively scales information technology is more appropriate to consider the private droplets, which in turn consist of water molecules, which consist of atoms, which consist of protons and electrons etc.

The scale of an image landmark is its (crude) diameter in the paradigm. Information technology is denoted by σ, which is measured in pixels, yous can remember scale invariance as that we tin can detect like landmarks even if their calibration is dissimilar.

So how does SIFT achieves scale invariance?
Do you still remember the pyramids ?

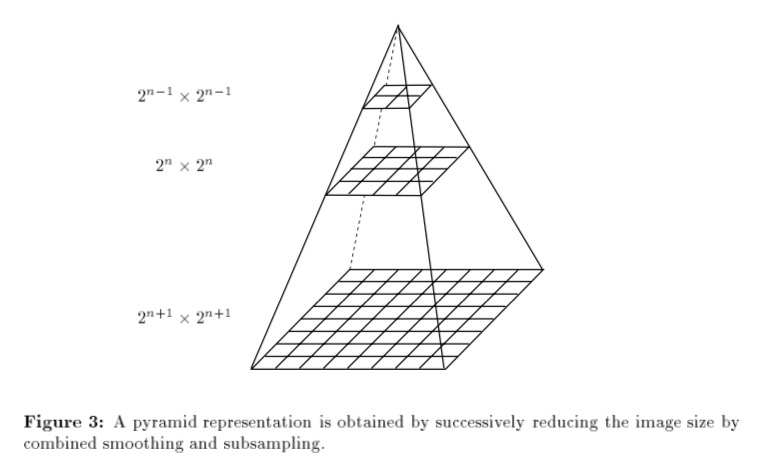
Nosotros can find the features nether various prototype sizes.
Besides, nosotros can also use the Laplacian of Gaussian(LoG) with dissimilar σ to achieve this.

Let's first take a await at LoG.
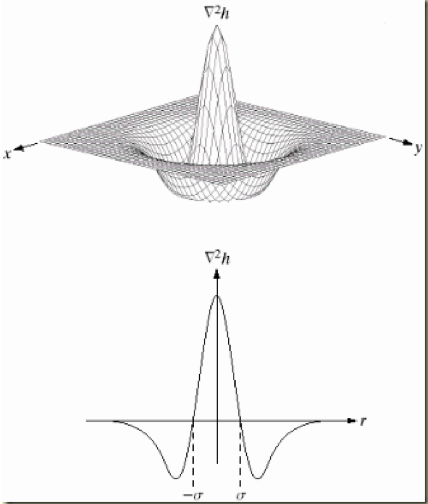
Equally Li Yin's commodity indicates, the LoG operation goes like this. You have an paradigm, and blur it a footling (using Gaussian kernel). And so, you calculate the sum of second-society derivatives on information technology (or, the "Laplacian"). This locates edges and corners on the image. These edges and corners are good for finding keypoints (notation that we want a keypoint detector, which means we volition practice some extra operations to suppress the edge). LoG is often used for blob detection (I will explicate information technology later).
Remember the human relationship between convolution and differentiation.

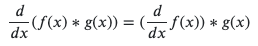
We tin can just convolve the image with the 2d derivatives of Gaussian, and sum them (or only convolve using LoG).

Have a 1-D case, f is a scanline of an image (i.e. the pixel array from a line of an image).

You can come across that if we use LoG to detect the edge, we demand to find the zero crossing the LoG response. Instead of finding the nothing crossing, we can use LoG to notice the blob as we said above.

Aha! We don't need to find the zero crossing anymore, we can notice the extrema (maxima and minima) instead.
However, the LoG is non truly scale invariant, yous tin can find that: Laplacian response decays equally scale increases:

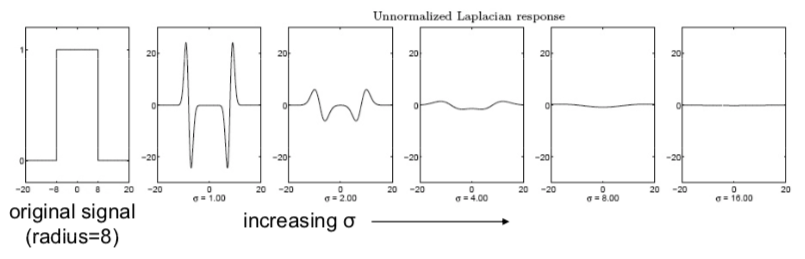
So why does this happen?

I will give y'all two ways to explain that:

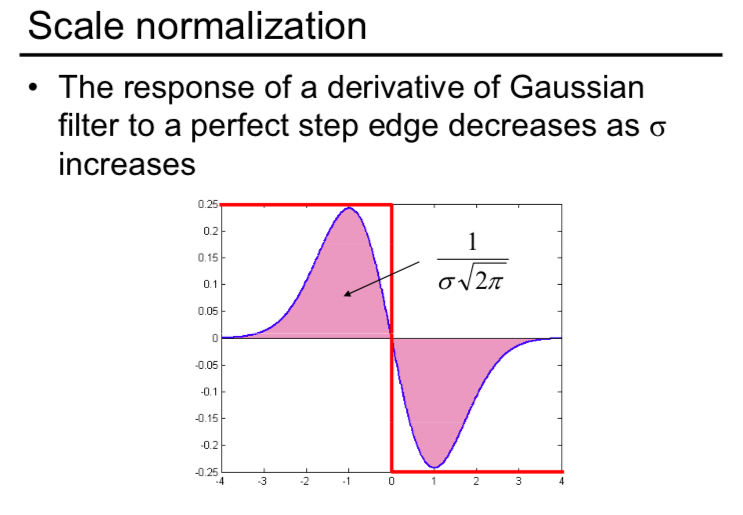
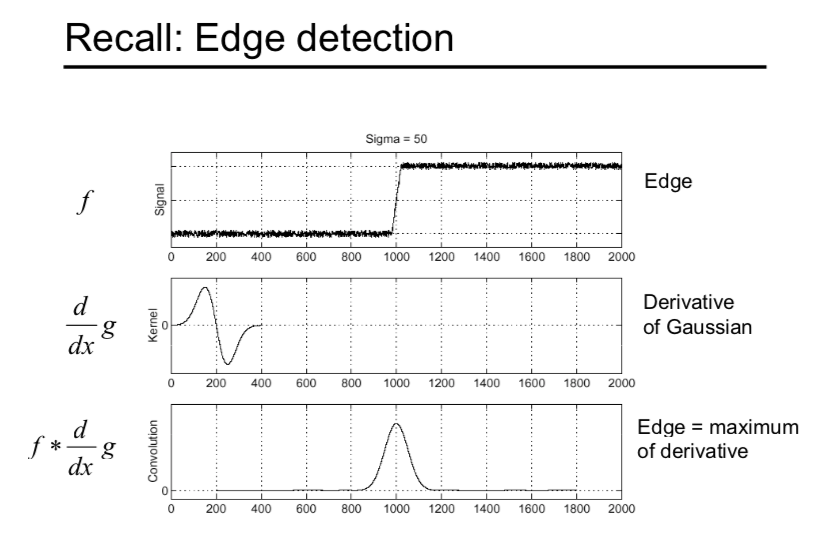
• The response of a derivative of Gaussian filter to a perfect footstep edge decreases as σ increases.
• To go on response the same(scale-invariant), must multiply Gaussian derivative past σ.
• Laplacian is the 2d Gaussian derivative, so information technology must be multiplied past σ2.

If you are satisfied with the above explanation and you lot are tired of struggling with some mathematical concepts, feel gratis to skip the following explanation.

Some other explanation is from this tutorial pdf.

Consider a racket-gratuitous image edge I(x) = u(x − x0), u is the unit step function . To discover edges previously, nosotros convolved them with a derivative of Gaussian and then looked for a peak in the response. Suppose we define a scale space by convolving I(x) with a family of the first derivative of Gaussian filters, where a family unit means we have a family of σ.

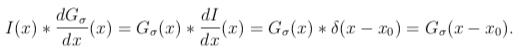
At the location of the border x = x0, nosotros accept

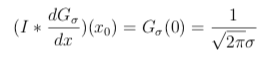
which depends on σ.

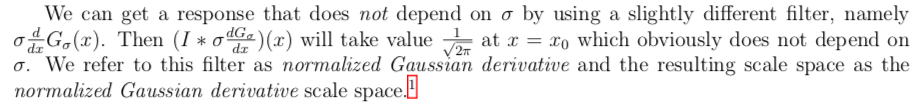
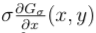
If we have a 2D paradigm, then we ascertain the normalized derivative filter in the same way, namely

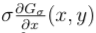
and similarly for y. Exactly the same arguments as above are used to testify that the
value at a horizontal or vertical edge volition be contained of σ. Using these filters, one defines the normalized gradient scale space in the obvious mode, and one will find that the slope at an edge of arbitrary orientation volition be independent of σ.
Now hither comes the 2nd derivates
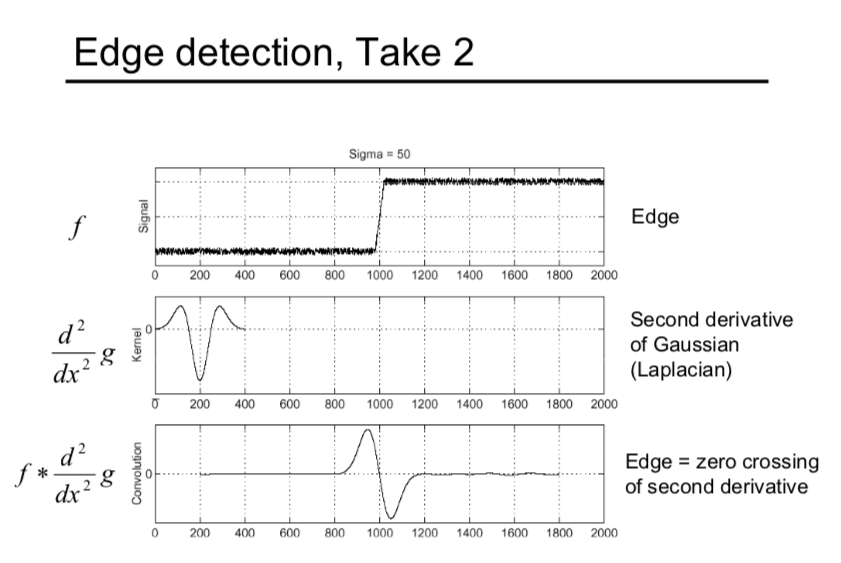
Nosotros know that if we filter a (noise-free) edge, I(x) = u(x − x0), with the first derivative of a Gaussian then we get a superlative response at the location of the edge. Information technology follows immediately that if we were to filter the edge with the 2d derivative of a Gaussian

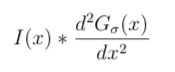
so the response would exist aught at the location of the edge.
The second derivative of a Gaussian filter, and its 2d equivalent, have been very important in computer vision likewise equally in human being vision modeling, and was the footing for an influential early theory of edge detection. The response of this filter to the edge prototype is:

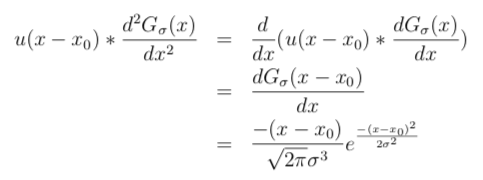
and note that the response is indeed 0 when 10 = x0, equally we expect.
Where exercise the peaks occur? Taking the derivative we get

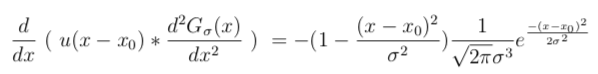
and set it to 0. The peak thus occurs when

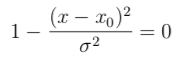
that is, ten=x0±σ. Substituting, we see that the value of the summit is

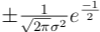
As we did with the first derivative filter, we tin can normalize the second derivative filter by multiplying by σ2, so the normalized second derivative filter is defined.

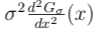
This cancels the σ^(−2) dependence in the top of the peaks. Thus we encounter that if nosotros filter an edge with a normalized second derivative of a Gaussian (as defined above), then there is a naught-crossing at the location of the border and there are peaks (positive and negative) at a distance ±σ away from the edge, but the top of the peaks doesn't depend on σ.

In summary, we need to multiply the LoG with σ2 to get the true calibration invariance. Post-obit is the upshot:

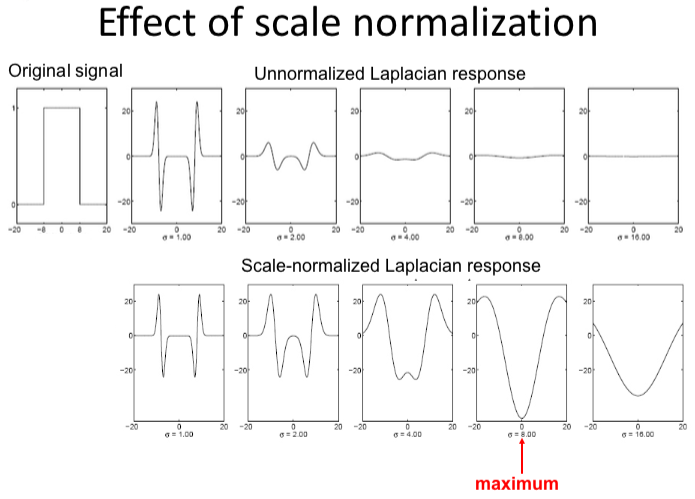
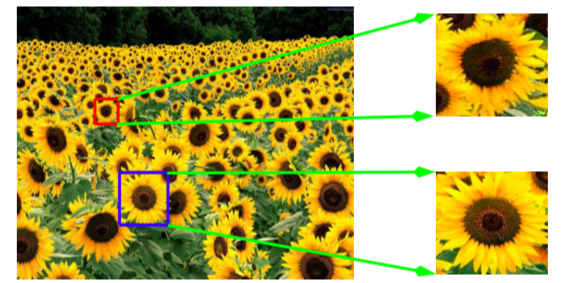
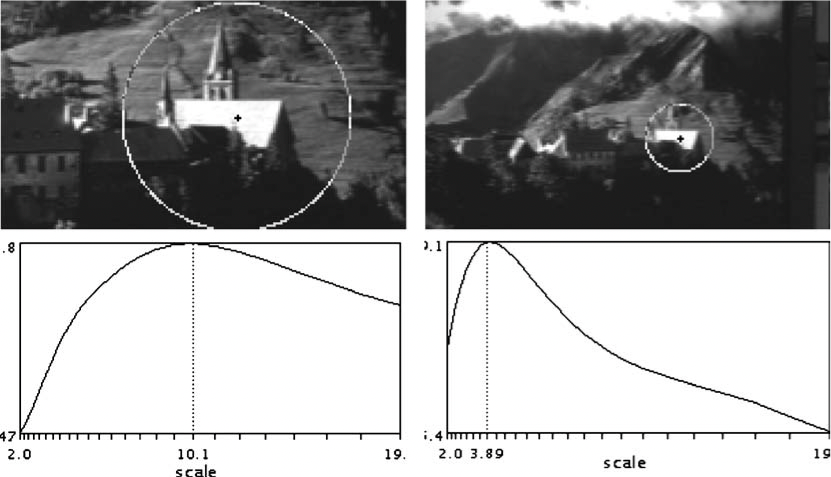
Now we tin notice the landmark at appropriate scale, information technology's actually important because nosotros need to describe this region in later steps, and we need to choose its surrounding region based on that scale, as shown in following:

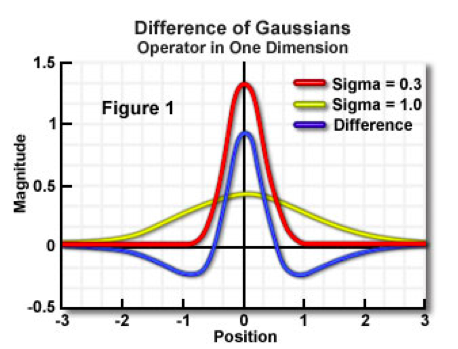
In practice, the Laplacian is approximated using a Divergence of Gaussian (Canis familiaris).

The human relationship betwixt Canis familiaris and σ2LoG can exist understood from the oestrus diffusion equation (parameterized in terms of σ rather than the more usual t = σ2, y'all can come across page 11 for more details:

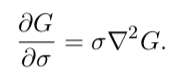
From this, we see that LoG can be computed from the finite difference approximation to ∂K/∂σ, using the difference of nearby scales at kσ and σ:

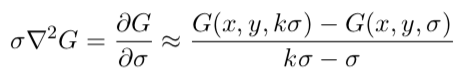
and therefore:

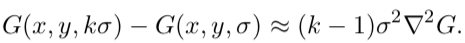
This shows that when the Dog function has scales differing past a constant gene information technology already incorporates the σ2 scale normalization required for the scale-invariant Laplacian. The gene (one thousand − 1) in the equation is a constant over all scales and therefore does not influence extrema location.

Above all, SIFT combines the pyramids and different σ-space to discover blobs under different scales.

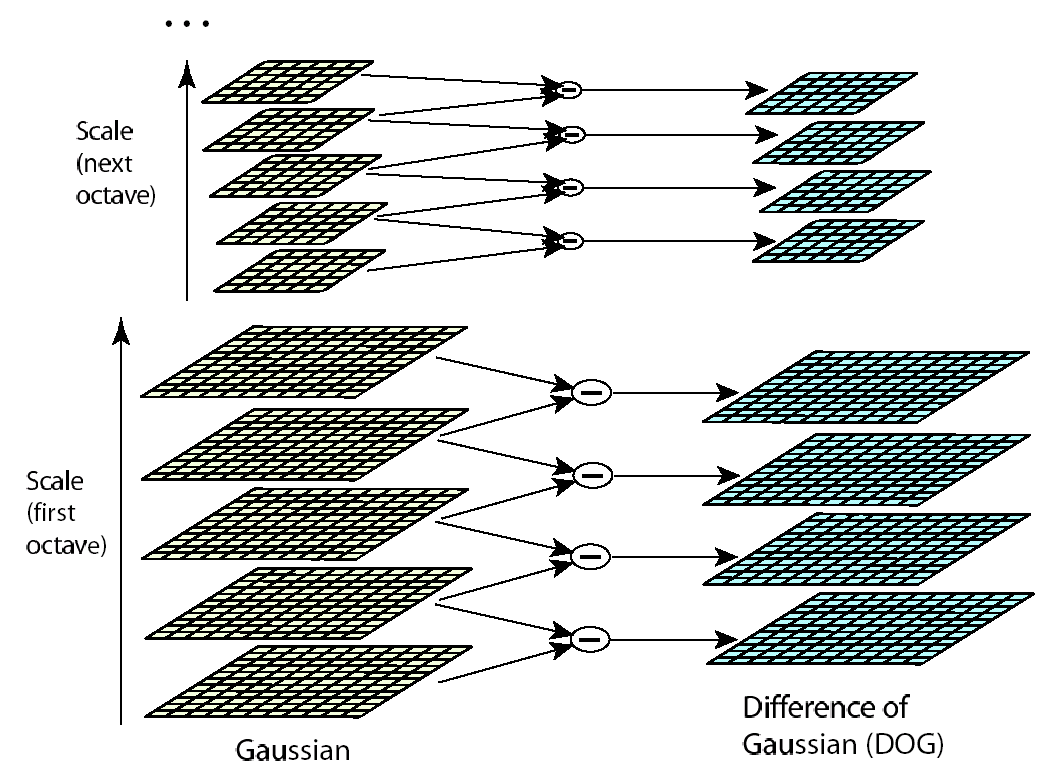
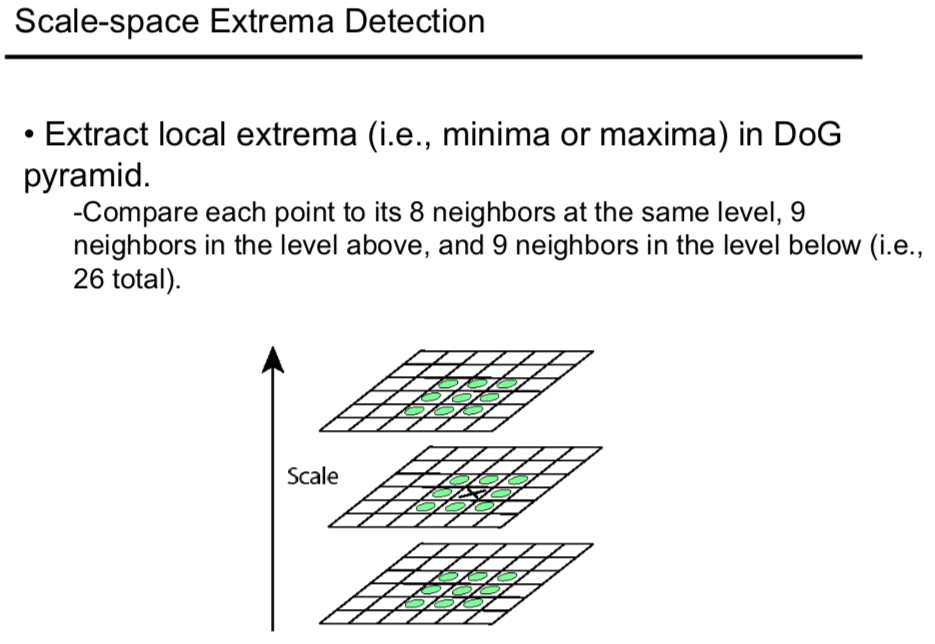
Note that the extrema are the maxima or minima around three dimensions (i.e. ten,y,σ).

Feature point localization (sub-pixel localization)

This part is mainly from N Campbell'south article.
After step one, we notice some key-points which are coarsely localized, at best to the nearest pixel, dependent upon where the features were constitute in the scale-space. They are also poorly localized in scale since σ is quantized into relatively few steps in the calibration-space. The second stage in the SIFT algorithm refines the location of these characteristic points to sub-pixel accuracy whilst simultaneously removing any poor features. The sub-pixel localization proceeds by plumbing equipment a Taylor expansion to fit a 3D quadratic surface (in x,y, and σ) to the local expanse to interpolate the maxima or minima. Neglecting terms above the quadratic term, the expansion of the DoG is given in following where the derivatives are evaluated at the proposed point z0=[x0,y0,σ0]T and z=[δx,δy,δσ]T is the showtime from this betoken.

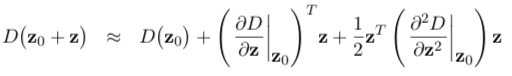
The location of the extremum zˆ is and so determined by setting the derivative with respect to z equal to zeros:

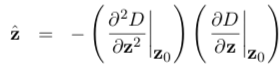
The parameters may exist estimated using standard difference approximations from neighbouring sample points in the DoG resulting in a three × iii linear organisation which may exist solved efficiently. The process may need to be performed iteratively since if whatever of the computed offset values move past more than half a pixel it becomes necessary to reevaluate z^ since the appropriate neighborhood for the approximation volition have inverse. Points which to not converge quickly are discarded as unstable.
The value at the localized extremum may be interpolated,

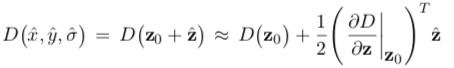
and any points with a value below a certain threshold rejected as depression contrast points.
A final test is performed to remove any features located on edges in the image since these will suffer an ambiguity if used for matching purposes. A pinnacle located on a ridge in the Canis familiaris (which corresponds to an edge in the image) will have a large principle curvature across the ridge and a depression one along with it whereas a well-defined peak (blob) will have a large principle curvature in both directions . The Hessian H in ten and y

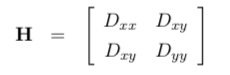
is evaluated for the characteristic betoken, over again using a local divergence approximation, and the ratio of the eigenvalues λ1 and λ2, which stand for to the master curvatures, compared to a threshold ratio r as in

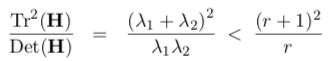
and high ratio points rejected.
This is a petty similar to Harris, which cares about the derivate distribution of the region around the chosen point. (You can become more information from this pdf)

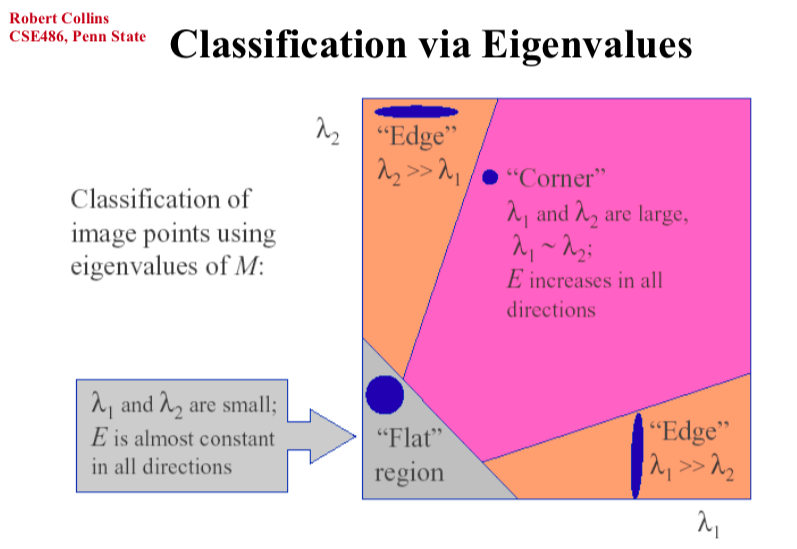
Nonetheless, the eigenvalues of Hessian H correspond to the master curvatures. So how?

This pdf gives an excellent explanation.
Let'south assume we have a surface Chiliad in R³ that is given by the graph of a smooth role z = f(x,y). Assume that M passes through the origin, p, and its tangent plane there is the {z = 0} plane (information technology's virtually truthful for the detected blob, recollect about the sunflowers). Let N = (0,0,1), a unit normal to M at p.

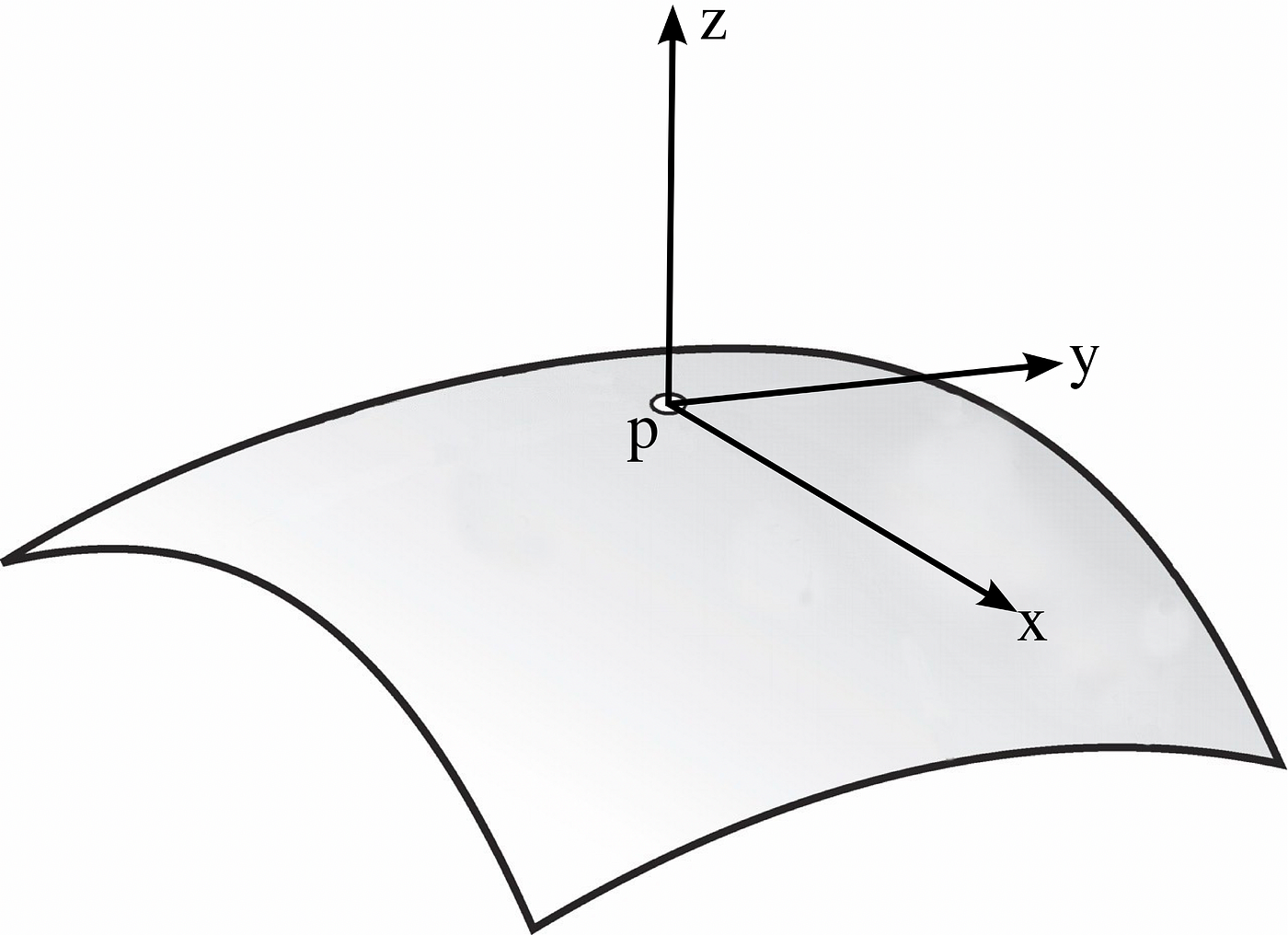
Allow v be a unit vector in TpM, say v = (v1,v2,0). Permit c be the parameterized curve given past slicing Thousand through the airplane spanned by v and North:

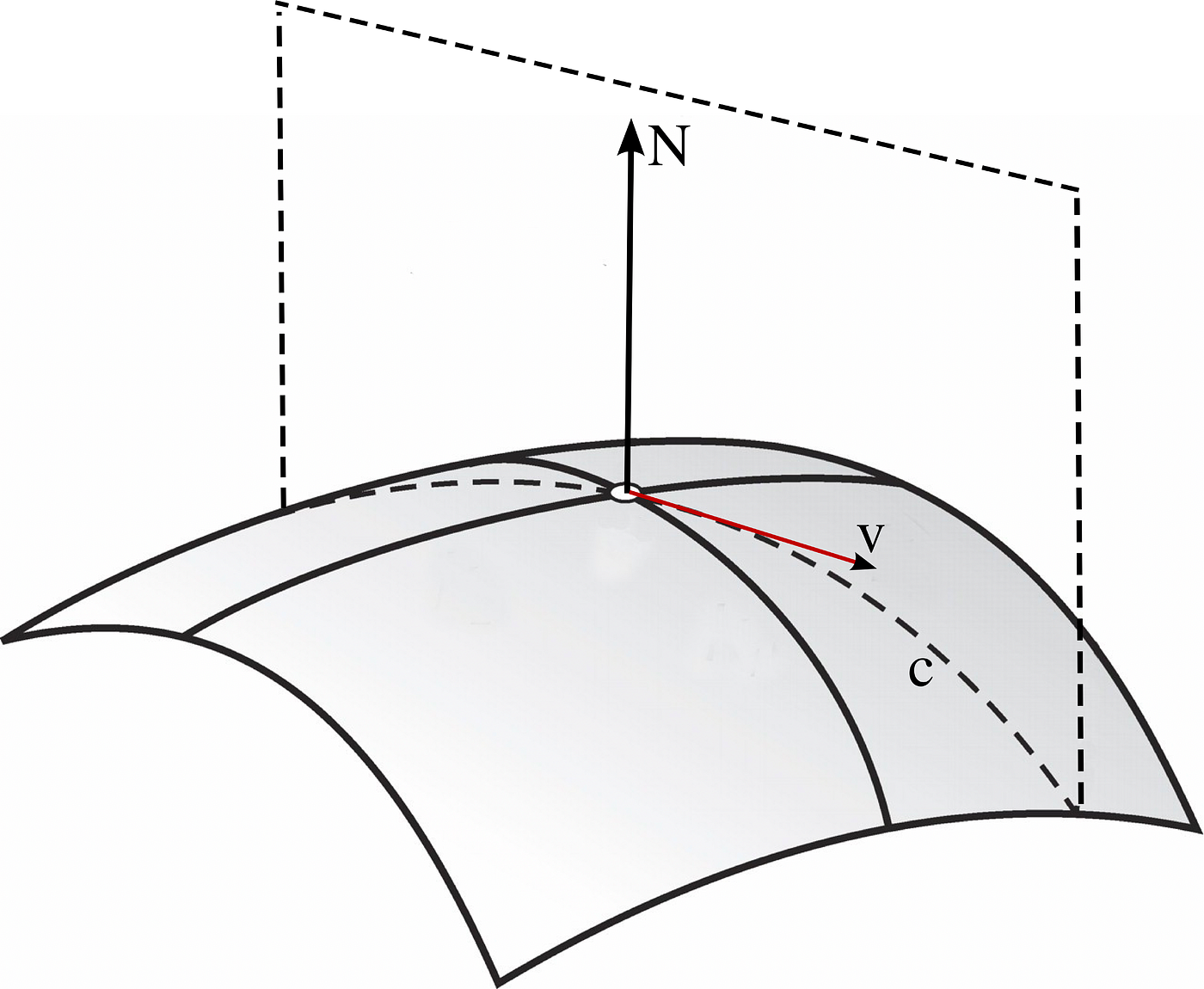
That is:

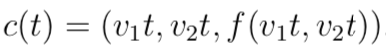
Now we tin calculate the curvature of c along the five = (v1,v2,0) management. κv is the reciprocal of the radius of the osculating circle to c at p.

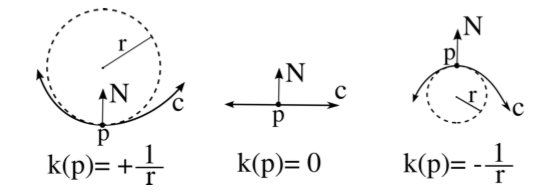
κv = c′′(t)|t=0
So,

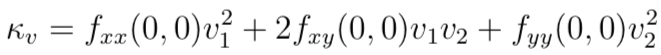
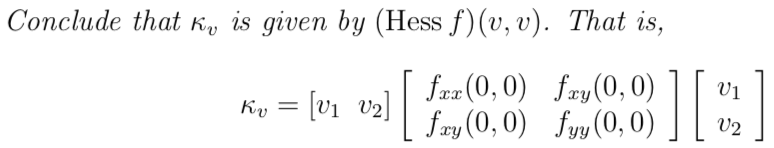
The primary curvatures of the surface at p will be the largest and smallest possible values λ1,λ2 of κv (equally v ranges over the possible unit of measurement tangent vectors). If you don't sympathize this argument, you can take a look at the excellent blog about PCA.

Orientation Assignment

Of course, we will utilize the Histogram of Oriented Slope (HOG)

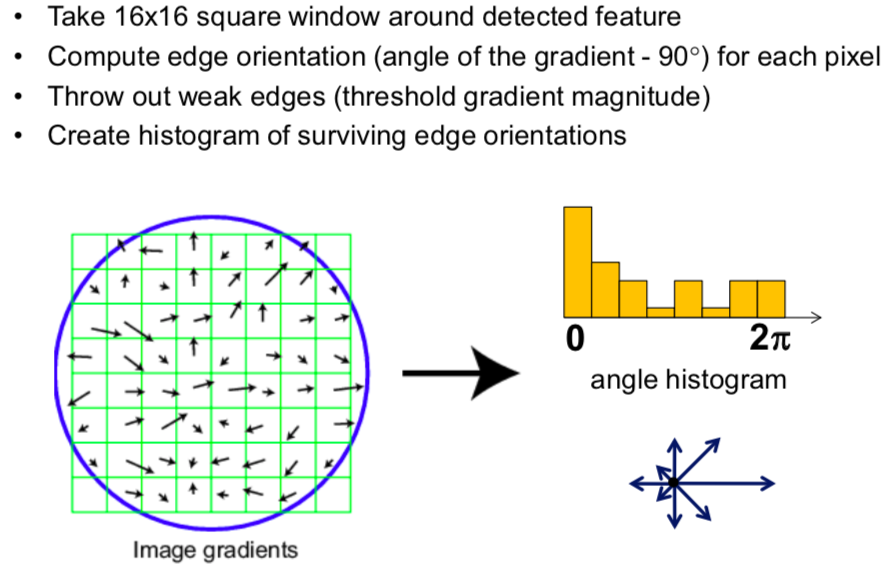
An orientation histogram is formed from the gradient orientations of sample points within a region around the keypoint. The orientation histogram has 36 bins covering the 360-degree range of orientations. Each sample added to the histogram is weighted by its gradient magnitude and past a Gaussian-weighted circular window with a σ that is one.5 times that of the scale of the keypoint.

Feature descriptor generation

The final stage of the SIFT algorithm is to generate the descriptor which consists of a normalized 128-dimensional vector. At this stage of the algorithm, we are provided with a list of characteristic points which are described in terms of location, scale, and orientation. This allows us to construct a local coordinate organization around the feature point which should exist similar across unlike views of the same characteristic.
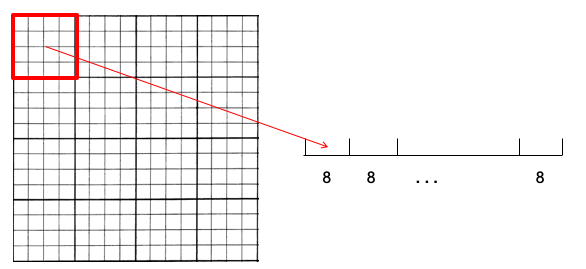
The descriptor itself is a histogram formed from the gradient of the grayscale image. A 4×4 spatial filigree of gradient angle histograms is used. The dimensions of the grid are dependent on the feature point calibration and the grid is centered on the feature betoken and rotated to the orientation determined for the keypoint. Each of the spatial bins contains an angle histogram divided into 8. (128=4×4×8). The prototype gradient magnitude and angle are once more generated from the calibration-infinite.

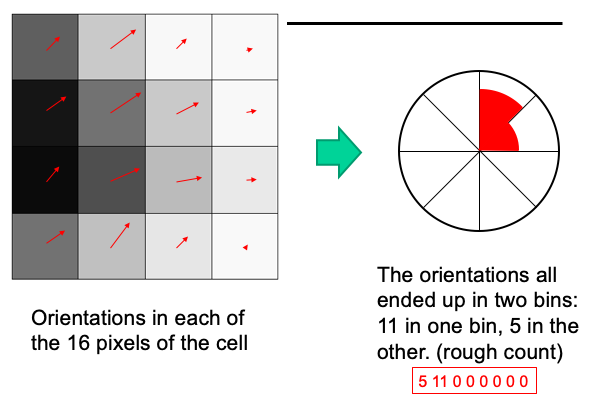
The gradient angle at each pixel is then added to the corresponding angle bin in the appropriate spatial bin of the grid. The weight of each pixel is given by the magnitude of the slope as well as a scale-dependent Gaussian (σ equal to one half the width of the descriptor window) centered on the feature indicate as shown as the blueish circle. The purpose of this Gaussian window is to avoid sudden changes in the descriptor with minor changes in the position of the window, and to give less emphasis to gradients that are far from the center of the descriptor, as these are nearly affected by misregistration errors.

During the histogram germination, trilinear interpolation is used to add each value, that is an interpolation in x, y and θ. This consists of interpolation of the weight of the pixel across the neighboring spatial bins based on distance to the bin centers also as interpolation beyond the neighboring bending bins. The effect of the interpolation is demonstrated in the following effigy.

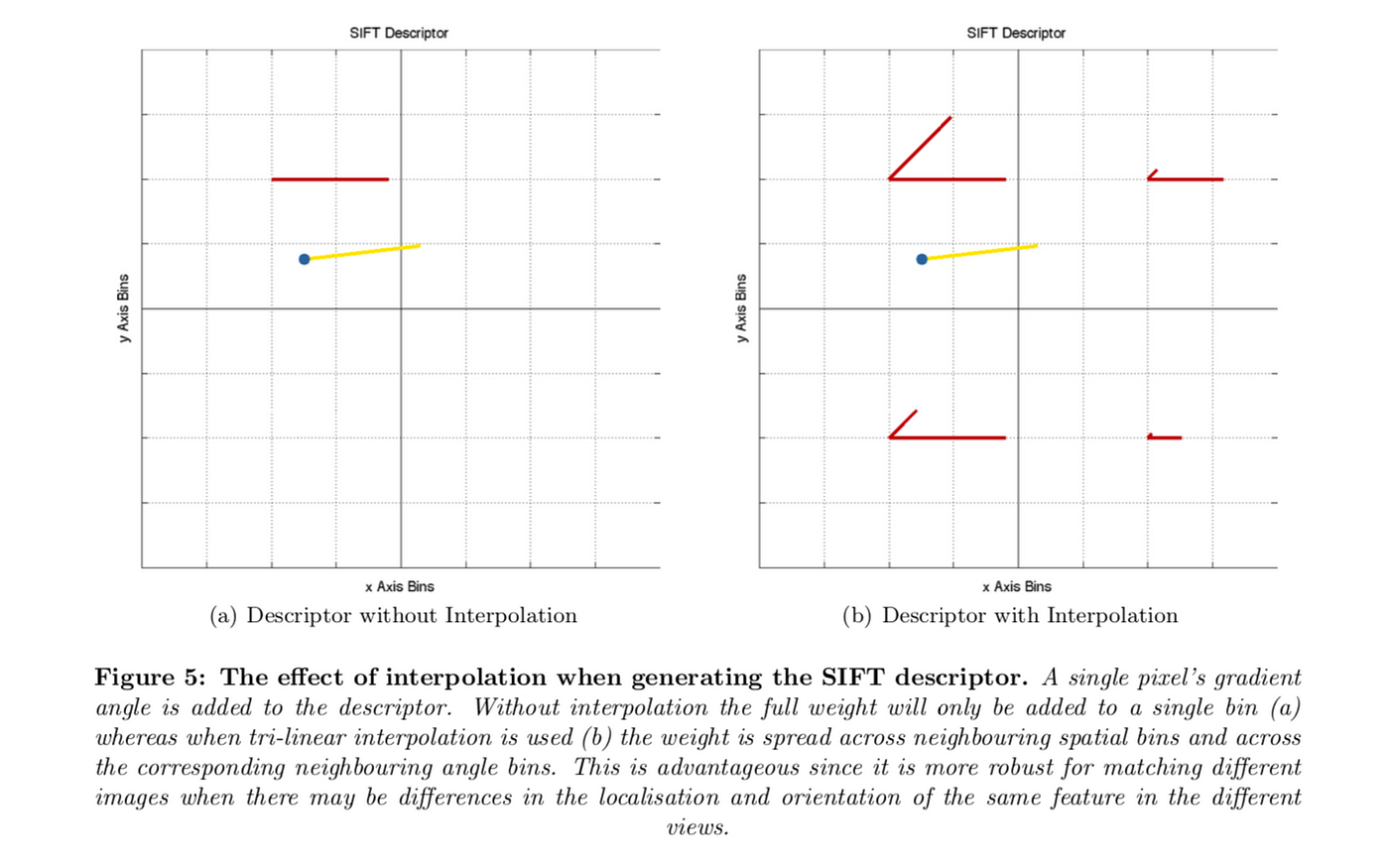
It is used to avoid all purlieus furnishings in which the descriptor abruptly changes as a sample shifts smoothly from existence within i histogram to another or from i orientation to another. Therefore, trilinear interpolation is used to distribute the value of each gradient sample into next histogram bins. In other words, each entry into a bin is multiplied by a weight of 1 − d for each dimension, where d is the altitude of the sample from the central value of the bin as measured in units of the histogram bin spacing.

Finally, the characteristic vector is modified to reduce the effects of illumination change. Start, the vector is normalized to unit length. A change in image dissimilarity in which each pixel value is multiplied by a constant will multiply gradients by the same constant, so this contrast change will exist canceled past vector normalization. A effulgence change in which a constant is added to each paradigm pixel will not bear upon the gradient values, as they are computed from pixel differences. Therefore, the descriptor is invariant to affine changes in illumination. Nonetheless, non-linear illumination changes can also occur due to photographic camera saturation or due to illumination changes that affect 3D surfaces with differing orientations by different amounts. These furnishings can cause a large change in relative magnitudes for some gradients, but are less likely to affect the slope orientations. Therefore, we reduce the influence of large gradient magnitudes past thresholding the values in the unit characteristic vector to each exist no larger than 0.2, and then renormalizing to unit of measurement length. This means that matching the magnitudes for large gradients is no longer equally of import, and that the distribution of orientations has greater emphasis. The value of 0.2 was adamant experimentally using images containing differing illuminations for the same 3D objects.

That's all, I really hope that this commodity volition help you empathise the SIFT algorithm. Because I am still a learner of Computer Vision, if you have any questions or suggestions, feel complimentary to contact me. I will be really happy if you can bespeak out my mistake. 🤪

parkerplaragnight45.blogspot.com

Source: https://towardsdatascience.com/sift-scale-invariant-feature-transform-c7233dc60f37

Share this post